Answer-
Sally's monthly payments is $165.53
Solution-
The cost of the sailboat = $5,275
Down payment amount = $500
The amount she financed = 5275-500 = $4775
We know that,
![\text{PV of annuity}=P[(1-(1+r)^(-n))/(r)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/cy9ahob6x9t9575dv6pue9ne54n5zfwxxa.png)
Here,
Present Value of annuity = $4775
r = rate of interest = 15% annual =
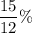 monthly = 1.25% monthly
monthly = 1.25% monthly
n = time period = 36
Putting the values,
![\Rightarrow 4775=P[(1-(1+0.0125)^(-36))/(0.0125)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/7fbnkveqx617qz0z9vysm090arv4zohbk6.png)
![\Rightarrow 4775=P[(1-(1.0125)^(-36))/(0.0125)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/nheydfljszx2fot9fbth86qnmsq1z0mzxk.png)
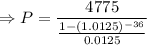
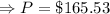
Therefore, Sally's monthly payments is $165.53