Question

A population of bacteria is growing according to the exponential model P = 100e.70t, where P is the number of colonies and t is measured in hours. After how many hours will 300 colonies be present? [Round answer to the nearest tenth.]

A) 0.7
B) 1.6
C) 5.7
D) 7.2

Answer 1

T=(log(300÷100)÷log(e))÷0.7
T=1.6

Answer 2

The correct option is B). 1.6 years

Explanation:

The model for the population of bacteria is growing by :

`P = 100\cdot e^(0.70t)`

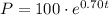
where P is the number of colonies and t is measured in hours.

Now, we need to find after how many hours will 300 colonies be present

So, Putting value of P = 300 in the above model and obtain the value of t

`\implies 300=100\cdot e^(0.70t)\\\\\implies 3=e^(0.7t)\\\\\text{taking natural log ln on both the sides}\\\\\implies \ln 3=\ln e^(0.7t)\\\\\implies \ln 3=0.7t\\\\\implies t=(\ln 3)/(0.7)\\\\\implies t=1.6\:\: years`

Therefore, The correct option is B). 1.6 years