Consider the differential equation
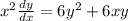
which may be considered either as a homogenous equation or as a Bernoulli equation.
If we make the substitution
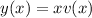
relevant to homogenous equations, we obtain
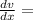
If we make the substitution
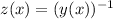
relevant to homogenous equations, we obtain
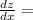
Using either (or both) of these methods, solve the initial value problem for the above equation where y(3)=6. Find the interval of validity of this solution.