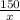Question

Katalin drove 180 miles on her vacation. She drove an average of 1.5 times faster on the second 90 miles of her trip than she did on the first 90 miles of her trip. Which expression represents the time she spent driving? Let x = her speed on the first half of the trip.

A. 150/x
B. 300/x
C. 150x
D. 225/x

Answer 1

Answer: 150/x

Step-by-step explanation: JeanaShupp is correct. Just took the quiz.

Answer 2

Answer: A)
`(150)/(x)`

Explanation:

We know that
`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

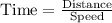
Let x be her speed on the first half of the trip.

Then for first half , the time taken by her is given by :_

`t_1=(90)/(x)`

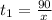
For second half , the time taken by her is given by :_

`t_2=(90)/(1.5x)\\\\\Rightarrow\ t_2=(60)/(x)`

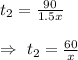
Now, the total time taken by her is given by :_

`t=t_1+t_2\\\\\Rightarrow t=(90)/(x)+(60)/(x)\\\\\Rightarrow t=(90+60)/(x)\\\\\Rightarrow t=(150)/(x)`

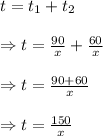
Hence, the expression represents the time she spent driving is
`(150)/(x)`