Step-by-step explanation
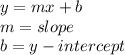
- Calculate the slope with two given coordinate by using rise over run.
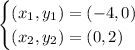
These two coordinate points are part of the graph and can be used to find the slope.

Substitute the coordinate points in the formula.
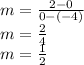
Therefore, the slope is 2.
Rewrite the equation in slope-intercept.
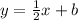
- Calculate the y-intercept by substituting any given points in new rewritten equation.
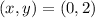
I will be substituting these coordinate points in the equation.
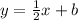
Substitute x = 0 and y = 5 in the equation.
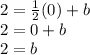
Therefore the y-intercept is (0,2).
Rewrite the equation.
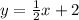
Answer

If you have any questions related to the answer, feel free to ask me via comment.