Question

jordan is considering buying her first home. the house she is interested in buying is priced at 169,000. jordan qualifes for a 30-year mortgage at 5.95%. what will be her monthly mortgage payment

Answer 1

Use the formula of the present value of annuity ordinary
pv=pmt [(1-(1+r/k)^(-kn))÷(r/k)]
Solve for pmt (monthly payment)
Pmt =pv÷[(1-(1+r/k)^(-kn))÷(r/k)]
Pmt=169,000÷((1−(1+0.0595÷12)^(
−12×30))÷(0.0595÷12))=1,007.81..Answer

Answer 2

Monthly payment is = $1006.75 approx

Explanation:

The price or principle is = $169000

time or n = 30*12=360

rate = 5.95/12/100=0.00495

The EMI formula is given as:

`(p*r*(1+r)^(n) )/((1+r)^(n)-1 )`

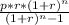
Now putting the values in the formula we get,

`(169000*0.00495*(1.00495)^(360) )/((1.00495)^(360)-1 )`

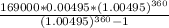
Monthly payment is = $1006.75 approx