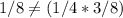Question

A class of 160 students contains 40 honor students, 60 athletes, and 80 who are neither athletes nor honor students. From the entire group a student is chosen at random. The fraction equation that proves the events "honor student" and "athlete" are not independent is ____.

Answer 1

There are 160 total number of students.
Other givens are the following:
40 are honor students
60 are athletes
80 are either honor or athletes
The probability that the chosen student is an athlete:
P = 60/180
P= 0.375
The probability that the chosen student is an honor:
P=40/160
P=0.25

Answer 2

1 / 8 is not equal to 3 / 32

Explanation:

Total number of Students in the class =160

Out of which,

Number of honor students = 40

Number of Athletes = 60

The probability of the event "honor student" is: 40/160=1/4 P(A)

The probability of the event "athlete student" is: 60/160=3/8 P(B)

Two events A and B are Said to be Independent, if

⇒P (A ∩ B)=P (A) × P (B)

Total Number of students in the class - n (A ∪ B)= 80

180=n(A∪B)

⇒n (A ∪ B)=80

⇒80= 40 +60 - n(A ∩ B)

⇒n (A ∩ B)= 20

P (A ∩ B) = 20/160=1/8

Lets check: P (A ∩ B)=P (A) × P (B)

`1/8\\eq (1/4*3/8)`

`1/8\\eq 3/32`