Answer:

Explanation:
Given: The first term of Geometric series : a=1
The seconds term of Geometric series :
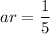
The common ratio between the terms is given by :-
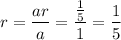
We know that the sum of infinite geometric series is given by :-
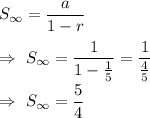
Hence, the sum of the given infinite series =
