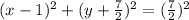Question

*NEED HELP ASAP*

The equation x^2 + y^2 - 2x + 7y + 1 = 0
can be rewritten as which of the following equations?

A. (X - 1)^2 + (Y - 7/2)^2 = (7/2)^2
B. (X + 1)^2 + (Y + 7/2)^2 = (7/2)^2
C. (X + 1)^2 + (Y + 7)^2 = 7^2
D. (X - 1)^2 + (Y - 7)^2 = 7^2

Answer 1

x^2 + y^2 - 2x + 7y + 1 = 0


(x^2 - 2x) + (y^2 + 7y) + 1 = 0


(x^2 - 2x + 1) + (y^2 + 7y) + 1 = 0+1


(x^2 - 2x + 1) + (y^2 + 7y + 49/4) + 1 = 0+1+49/4


(x - 1)^2 + (y + 7/2)^2 + 1 = 0+1+49/4


(x - 1)^2 + (y + 7/2)^2 + 1-1 = 0+1+49/4-1


(x - 1)^2 + (y + 7/2)^2 = 49/4


(x - 1)^2 + (y + 7/2)^2 = (7/2)^2


The final answer is choice B

Answer 2

The correct option B
`(x -1)^(2) + (y +(7)/(2))^(2) = ((7)/(2))^(2)`

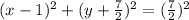
Explanation:

We need to find out the correct option which is similar to the expression;

`x^(2) + y^(2)- 2x + 7y + 1 = 0`

combine the similar variable together

`(x^(2) - 2x) + (y^(2) + 7y) + 1 = 0`

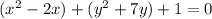
Add 1 both the sides,

`(x^(2) - 2x + 1) + (y^(2) + 7y) + 1 = 0+1`

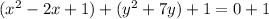
Add both the sides by
`(49)/(4)`

`(x^(2) - 2x + 1) + (y^(2) +(49)/(4)+ 7y) + 1 = 0+1 + (49)/(4)`

`(x^(2) - 2x + 1) + (y +(7)/(2))^(2) + 1 = 0+1 + (49)/(4)`

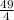
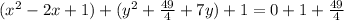
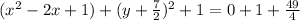
Subtract both the sides by 1,

`(x^(2) - 2x + 1) + (y +(7)/(2))^(2) + 1-1 = 0+1 + (49)/(4)-1`

`(x^(2) - 2x + 1) + (y +(7)/(2))^(2) = (49)/(4)`

`(x -1)^(2) + (y +(7)/(2))^(2) = ((7)/(2))^(2)`

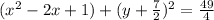
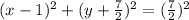
This is equivalent to option B

Therefore the correct option B
`(x -1)^(2) + (y +(7)/(2))^(2) = ((7)/(2))^(2)`