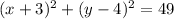Question

Write an equation for the translation of x^2+y^2=49 by 3 units left and 4 units up

Answer 1

(x+3)^2+(y-4)^2=49
If you need clarification, you can ask me.

Answer 2

`(x+3)^2+(y-4)^2=49`

Explanation:

Given :
`x^2+y^2=49`

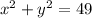
To Find: Write an equation for the translation of
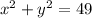`x^2+y^2=49` by 3 units left and 4 units up.

Solution:

`x^2+y^2=49`

`y^2=49-x^2`

`y=√(49-x^2)`

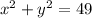
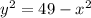
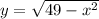
So,
`f(x)=y=√(49-x^2)`

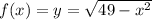
We are given that first is shifted towards 3 units left.

If the given function f(x) translated by b units left then

f(x)→f(x+b)

So,
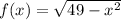`f(x)=√(49-x^2)` translated by 3 units left

So,
`f(x)=√(49-x^2)` →
`f(x+3)=√(49-(x+3)^2)`

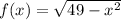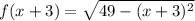
Now it is again translated by 4 units up.

If the given function f(x) translated by b units up then

f(x)→f(x)+b

`f(x+3)=√(49-(x+3)^2)`→
`f(x+3) +4 =√(49-(x+3)^2 )+4`

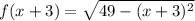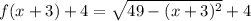
So, the function becomes :
`f(x)=y=√(49-(x+3)^2 )+4`

`y-4=√(49-(x+3)^2 )`

`(y-4)^2=49-(x+3)^2`

`(x+3)^2+(y-4)^2=49`

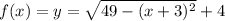
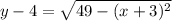
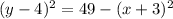
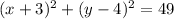
Hence an equation for the translation of
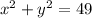`x^2+y^2=49` by 3 units left and 4 units up is
`(x+3)^2+(y-4)^2=49`