Question

Please help me with these

Answer 1

When we approach limits, we are finding values that are infinitesimally approaching this x-value. Essentially, we consider the approximate location that this root or limit appears. This is essential when it comes to taking Calculus, and finding the limit or rate of change of a function.

When we are attempting limits questions, there are several tests we attempt first.

1. Evaluate the limit by substituting the value of the x-value as it approaches the value (direct evaluation of a limit)
2. Rearrangement of the function, such that we can evaluate the limit.
3. (TRIGONOMETRIC PROPERTIES)

`\lim_(x \to 0) ((sinx)/(x)) = 1`

`\lim_(x \to 0) ((tanx)/(x)) = 1`
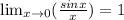
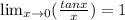
4. Using L'Hopital's Rule for indeterminate limits, such as 0/0, -infinity/infinity, or infinity/infinity.

For example:

1)
`\lim_(x \to 0)(√(x) - 5)/(x - 25)`

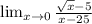
We can do this using the first and second method.
Method 1: Direct evaluation:

Substitute x = 0 to the function.

`(√(0) - 5)/(0 - 25)`

`= (-5)/(-25)`

`= (1)/(5)`

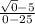
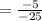
Method 2: Rearranging the function

We can see that x - 25 can be rewritten as: (√x - 5)(√x + 5)
By rewriting it in this form, the top will cancel with the bottom easily, and our limit comes out the same.


`\lim_(x \to 0)((√(x) - 5))/((√(x) - 5)(√(x) + 5))`

`= \lim_(x \to 0)(1)/((√(x) + 5))}`

`= (1)/(5)`

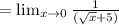
Every example works exactly the same way, and by remembering these criteria, every limit question should come out pretty naturally.