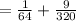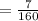Question

Ques. A biased die has a probability of 1/4 of showing a 5, while the probability of any of 1, 2, 3, 4, or 6 turning up is the same . If three such dice are rolled, what is the probability of getting a sum of atleast 14 without getting a 6 on any die ?

Answer 1

Since the addition of every probable event is equal to 1 and the probability of rolling a five is 1/4, then the probability of any of the other numbers is:


`\text{P(not five): }1 - (1)/(4) = (3)/(4)`

`\text{P(1) = P(2) = P(3) = P(4) = P(6): } (3)/(20)`

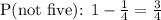
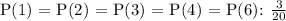
Now, the condition is that no die rolls a six. Thus, we need to limit our sample space from 216 down to 125, to ensure we're not rolling a six.

The ways we can reach 14 or greater are:
5, 5, 5
4, 5, 5 (which can occur in 3 ways)

Thus, our probability becomes:

`((1)/(4))^(3) + 3 \cdot (3)/(20) \cdot ((1)/(4))^(2)`

`= (1)/(64) + (9)/(320)`


`= (7)/(160)`

Answer 2

1/64 + 3/320 + 3/320 + 3/320 = 7/160

Answer: 7/160