Question

Bobby places a 4.75 cm tall light bulb a distance of 33.2 cm from a concave mirror. If the mirror has a focal length of 28.2, then what is the image height and image distance?

Answer 1

Step-by-step explanation:

Height of the light bulb, h = 4.75 cm

Distance between the light bulb and the concave mirror, u = -33.2 cm

Focal length of the mirror, f = -28.2 cm (negative always)

Let v is the distance between the image and the light bulb. It can be calculated as :

`(1)/(v)=(1)/(f)-(1)/(u)`

`(1)/(v)=(1)/(-28.2)-(1)/(-33.2)`

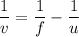
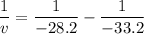
v = -187.24 cm

So, the image distance from the mirror is 187.24 cm.

The magnification of the mirror is given by :

`m=(-v)/(u)`

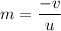
or

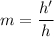`m=(h')/(h)`, h' is the size of image

`(-v)/(u)=(h')/(h)`

`(-(-187.24))/(-33.2)=(h')/(4.75)`

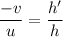
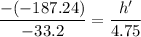
h = -26.78 cm

So, the height of the image is 26.78 cm and it is inverted. Hence, this is the required solution.

Answer 2

The image distance can be determined using the mirror equation: 1/f = 1/d_o + 1/d_i, where, f is the focal length, d_o is the object distance, and d_i is the image distance. Given that f = 28.2 and d_o = 33.2 cm, the value of d_i is calculated to be 187.248 cm. On the other hand, the image height is obtained using the magnification equation wherein, h_i/h_o = -d_i/d_o, where h_i is the image height and h_o is the object height. Using the given values, h_i is equal to -26.79 cm. Note that the negative sign indicates that the image is inverted.