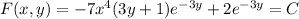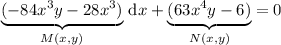
This equation is not exact, since
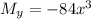
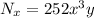
So we look for an integrating factor
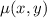
such that
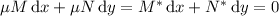
For this to be exact, we require
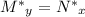
Differentiating both sides gives
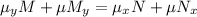

When we take
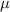
to be a function of either

or

, but not both, this partial differential equation reduces to one of the separable ordinary differential equations
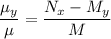
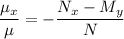
both of which can be solved directly for
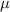
provided that the result on the right hand side of either ODE is a function of either only

or

, respectively.
The choice of which integrating factor
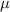
to look for is then decided by how easily the right hand side can be taken care of. We have

On the other hand, the integral resulting from an integrating factor

is more complicated/impossible to deal with. So, the integrating factor must be a function of

, which means
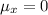
, and it satisfies

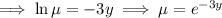
Distributing the integrating factor across the original ODE, we have
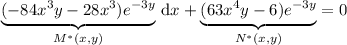
with partial derivatives
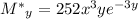
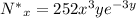
Thus the modified ODE is exact, as required. Now we try to find a solution of the form
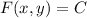
.

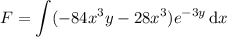
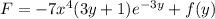
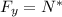
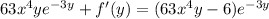
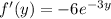

Therefore the general solution is