Question

What value of b makes the trinomial below a perfect square x^2-bx+100

Answer 1

its 20

Explanation:

Answer 2

1. Perfect square trinomials, are 2nd degree polynomials, of the form
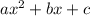
`a x^(2) +bx+c` so that
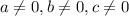
`a \\eq 0, b \\eq 0, c \\eq 0`, which can be written as perfect squares.

2. For example
`(x+1) ^(2) = x^(2) +2x+1 (3x-1)^(2)= (3x)^(2)-2(3x)+(-1) ^(2)= 9x^(2)-6x+1`

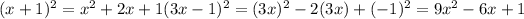
3. Thus
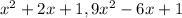
`x^(2) +2x+1, 9x^(2)-6x+1` are perfect square trinomials.

4.
`x^(2) -bx+100= x^(2) -bx+ 10^(2)= (x+10)^(2) or (x-10)^(2)`

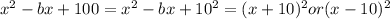
5. In the first case -b=20, so b=-20. In the second case, -b=-20, so b=20.

6. b∈{-20, 20}