Question

Which statement is correct about the function y = x2 – 2x – 143?

A) In factored form, the function is y = (x – 13)(x + 11), so the zeros of the function are x = –13 and x = 11.
B) In factored form, the function is y = (x + 13)(x – 11), so the zeros of the function are x = –13 and x = 11.
C) In factored form, the function is y = (x – 13)(x + 11), so the zeros of the function are x = 13 and x = –11.
D) In factored form, the function is y = (x + 13)(x – 11), so the zeros of the function are x = 13 and x = –11.

Answer 1

C is the correct answer. hope it helps. :)

Answer 2

In factor
`y=(x-13)(x+11)` and The zeros are x=13 and x=-11

C is correct.

Explanation:

Given:
`y=x^2-2x-143`

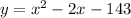
Factor the function,

`y=x^2-2x-143`

`y=(x^2-13x)+(11x-143)`

`y=x(x-13)+11(x-13)`

`y=(x-13)(x+11)`

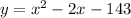
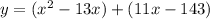
Factor of the given function is (x-13)(x+11)

If we find the zeros of the function, we will set each factor to zero.

x-13 = 0 and x+11=0

x=13,-11

The zeros of the function are 13 and -11

Hence, In factor
`y=(x-13)(x+11)` and The zeros are x=13 and x=-11