Question

Use the "mixed partials" check to see if the following differential equation is exact.

If it is exact find a function F(x,y) whose differential, dF(x,y) is the left hand side of the differential equation. That is, level curves F(x,y)=C are solutions to the differential equation
`(-3 e^(x) sin(y) + 3y) dx+(3y-3 e^(x) cos(y))dy=0`
Find
`M_(y) (x,y)` and
`N_(x) (x,y)` and it the equation is exact, find F(x,y) too.

Answer 1

`\underbrace{(-3e^x\sin y+3y)}_(M(x,y))\,\mathrm dx+\underbrace{(3y-3e^x\cos y)}_(N(x,y))\,\mathrm dy=0`

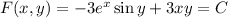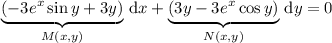
You have partial derivatives


`M_y=-3e^x\cos y+3`

`N_x=-3e^x\cos y`

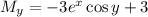
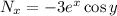
which are not equal, so the equation is not exact.

- - -

In case you meant to write


`N(x,y)=3x-3e^x\cos y`

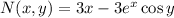
the equations would be exact, since


`N_x=3-3e^x\cos y`

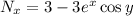
and in this case the ODE would be exact. I don't suppose it would hurt to demonstrate how to proceed with solving the ODE...

We're looking for a solution of the form
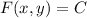
`F(x,y)=C`, which means that upon differentiating we have


`F_x\,\mathrm dx+F_y\,\mathrm dy=0\iff M(x,y)\,\mathrm dx+N(x,y)\,\mathrm dy=0`

which is to say that we can find
`F` by integrating
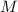
`M` and
`N`.


`F_x=M\implies F=\displaystyle\int M\,\mathrm dx`

`F=\displaystyle\int(-3e^x\sin y+3y)\,\mathrm dx`

`F=-3e^x\sin y+3xy+f(y)`

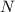
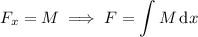
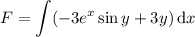
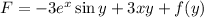
Differentiating with respect to
`y`, we have


`N=F_y`

`-3e^x\cos y+3x=3x-3e^x\cos y+f'(y)`

`0=f'(y)`

`\implies f(y)=C`

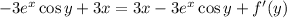
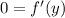
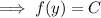
Thus the general solution (again, assuming you made a typo) would be


`F(x,y)=-3e^x\sin y+3xy+C=C`

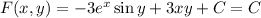
and since both
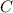
`C`s can be treated as arbitrary constants,


`F(x,y)=-3e^x\sin y+3xy=C`