Question

You have 7 balls that are each a different color of the rainbow. In how many distinct ways can these balls be ordered?

Answer 1

To start you have to write out the possible combinations 7,6,5,4,3,2,1. There are 7 numbers that can be combined in order to find the number of possibilities so 7*6*5*4*3*2*1 = 5,040

Answer 2

Answer: There are 5040 distinct ways that these balls can be ordered.

Explanation:

Since we have given that

Total number of balls = 7

According to question, each a different color of the rainbow in 7 balls.

We will use "Fundamental theorem of Counting " :

Number of distinct ways that these balls can be ordered is given by

`7!\\\\=7* 6* 5* 4* 3* 2* 1\\\\=5040`

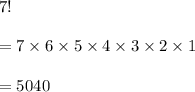
So, there are 5040 distinct ways that these balls can be ordered.