Question

Ms. Lunette has 18 students in her class. She wants to send 3 of these students to pick up books for the class.   How many combinations of 3 students can she choose?

816

4896

6

54

Answer 1

To answer this question, you'll need to use permutations and factorials.

Factorials are any integer with an ! after it. This means that all of the integers before that number are multiplied together with said number.

This question will use the following formula:

`(n!)/((n-r)!)`

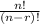
n represents the amount of items in a set, and r represents the amount of items in each combination within the set.

You have 18 students, and you can choose any combination of 3 students. Plug your values into the formula:

`n = 18, r = 3`

`(18!)/((18 - 3)!) = (18!)/(15!) = (15! * 16 * 17 * 18)/(15!)`

`(15! * 16 * 17 * 18)/(15!) = 16 * 17 * 18 = \boxed{4896}`

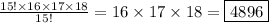
There are 4896 different combinations of students that Ms. Lunette can choose.