Question

Make a sketch of the graph the absolute value equation.Be sure to label the increments on your x and y axis the vertex as well as the intercepts.

Answer 1

Let the following function:

`f(x)=\text{ }(1)/(2)\textx+4`

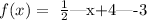
The graph of this function can be obtained by applying the respective function transformations to the absolute value function y = |x|. In this case, horizontal and vertical translations and vertical shortening were used on absolute value function y = |x|.

According to the function, the vertex can be obtained by solving the following equation:

`\text=0`

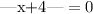
solving for x, we get:

`x\text{ = -4}`

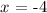
replacing this value into the function f(x) =y, we obtain:

`y\text{ = }-3`

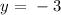
so that, the vertex of this function is on the point:

`(x,y)=(-4,-3)`

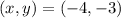
Now, to find the x-intercept, we set the equation of the function equal to 0 and then solve for x:

`0=\text{ }(1)/(2)\text-3`

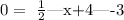
solving for x, we get two solutions:

`x=\text{ -10}`

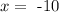
and

`x=\text{ }2`

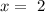
so that, the x-intercepts are the points:

`(x,y)=(-10,0)`

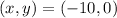
and

`(x,y)=(2,0)`

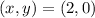
On the other hand, to find the y-intercept, we can evaluate the function f(x) at x=0, and then, we can solve for y:

`f(0)=\text{ }(1)/(2)\text-3=(1)/(2)\text-3\text{ = 2-3 = -1}`

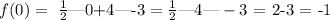
Then, the y-intercept is on the point:

`(x,y)=(0,-1)`

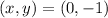
So that, we can conclude that the correct answer is: