Answer:
Option D.
Explanation:
The given function is
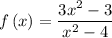
In this function the degree of numerator an denominator is same i.e., 2.
Horizontal Asymptotes: If the degree of numerator an denominator is same, then
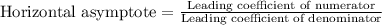
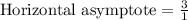
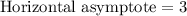
Horizontal asymptote is y=3.
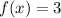
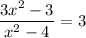
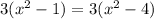
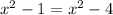
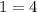
This statement is false for any value of x, therefore the graph does not cross the horizontal asymtote.
Vertical Asymptotes: Equate the denominator equal to 0, to find the vertical asymptotes.
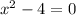
Add 4 on both sides.
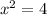
Taking square root on both sides.
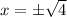

Vertical asymptotes are x=2 and x=-2.
The graph has two vertical asymptotes and one horizontal asymptote.
Therefore, the correct option is D.