We have the following trigonometric equation:
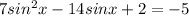
1. Now, we can rewrite the equation as follows:
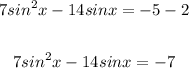
2. We have a common factor of 7 and sin(x). Then we have:
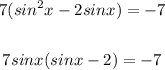
3. Now, we have:
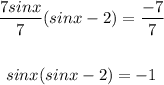
4. Now, if we have:
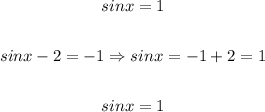
5. Then, the solutions for this equation will be - applying the inverse function of the sine function to both sides of the equation:
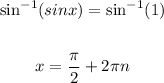
Therefore, in summary, the values that are solutions for this equation are:
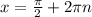
Where n is the any integer value.