Question

Enter a rule for each function, and B, and then compare their domains ranges, slopes and y-intercepts.Jeft, an electrician had a job that lasted 55 hours during which time he ears $32 per hour and charges a$24 service fee. The function() represents the amount Jeff eams in t hours Brendan also works as anelectrician The graph of B() shows the amount in dollars that Brendan earns as a function of timet inhours

Answer 1

The rule of the function J(t) is 32(earnings per hour)*t + 24 (service fee)

With the points given by Brendan we can find the slope and the intercept of the line. (0,20) and (4,140)

`m=(y2-y1)/(x2-x1)=(140-20)/(4-0)=(120)/(4)=30`

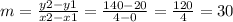
The slope is 30 and since the y-coordinate at x=0 is 20, we deduce the intercept is 20, so the rule for the function is B(t)= 30*t + 20

The domain of J(t) is [ 0, 55 ] , according to the information. ( he works 55 hours)

The domain of B(t) is [ 0, 4 ] according to the graph.

The range of J(t) is [ 24, J (55) ] replacing in the equation J(55) = 32*55+24 = 1784,

The range must be [ 24, 1784 ]

The range of B(t) is [ 20, 140 ] according to the graph.

The slope of J(t) is greater than the slope of B(t)

The y-intercept of J(t) is greater than the y-intercept of B(t)