Question

The service-time distribution describes the probability P that the service time of the customer will be no more than t hours. If m is the mean number of customers serviced in an hour, then Suppose a computer technical support representative can answer calls from 6 customers in an hour. What is the probability that a customer will be on hold less than 30 minutes?

Answer 1

95% is the answer to your question

Answer 2

Probability that a customer will be on hold less than 30 minutes is
`95`%

Explanation:

Complete question is

The service-time distribution describes the probability P that the service time of the customer will be no more than t hours. If m is

the mean number of customers services in an hour, then
`P = 1 - e^(-mt)`

. a. Suppose a computer technical support representative can answer calls from 6 customers in an hour. What is the probability

that a customer will be on hold less than 30 minutes?

Solution -

Given the equation of probability -

`P = 1 - e^(-mt)`

Where m is the average number of customers served in an hour

and t is the total time

Now, in this case m is equal to 6 as technical support representative ia bale to answer calls from 6 customers in an hour

and time t
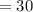`= 30` minutes
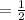`= (1)/(2)` hours

Substituting the given values in above equation, we get -

`P = 1 - e^{-6 *(1)/(2) }\\P = 1 - e^(-3)\\P = 1 - 0.04978\\P = 0.95`

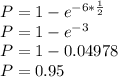
Probability that a customer will be on hold less than 30 minutes is
`95`%