Answer:
The y-coordinate of point W is

Explanation:
Step 1
Fin the slope of the line ST
we know that
The formula to calculate the slope between two points is equal to
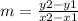
we have
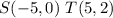
Substitute the values
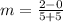
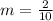
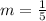
Step 2
Find the slope of the line WV
we know that
If two lines are perpendicular, then the product of their slopes is equal to minus one
so
 ------->
------->
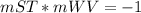
we have
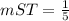
substitute the value and solve for mWV
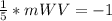
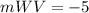
Step 3
Find the equation of the line WV into slope-intercept form

we have

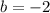 -------> see the graph Point V is the y-intercept of the line WV
-------> see the graph Point V is the y-intercept of the line WV
substitute

Step 4
Find the y-coordinate of the point W
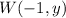
Substitute the the values of x and y of point W in the linear equation
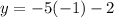
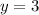
therefore
the y-coordinate of point W is
