Question

Use the standard enthalpies of formation for the reactants and products to solve for the ΔHrxn for the following reaction. (The ΔHf of Ca(OH)2 is -986.09 kJ/mol and liquid H2O is -285.8 kJ/mol.) Ca(s) + 2H2O(l) ---> Ca(OH)2 (s) + H2(g)

Answer 1

1. Remember (sum of products) - (sum of reactants)
So ΔHrxn = 2 ΔHf [H2(g)] + ΔHf [Ca(OH)2(s)] - 2 ΔHf [H2O(l)] - ΔHf [Ca(s)]
= 2*0 + -986.09 kJ/mol - 2*(-285.8 kJ/mol) - 0

Do the math and you'll have the answer. BTW the ΔHf [H2(g)] and ΔHf [Ca(s)] were 0 because these are elements in their standard states.

HOPE THIS HELPS ;)

Answer 2

Answer : The enthalpy change for this reaction is, -414.49 KJ

Solution :

The balanced chemical reaction is,

`Ca(s)+2H_2O(l)\rightarrow Ca(OH)_2(s)+H_2(g)`

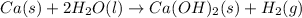
The expression for enthalpy change is,

`\Delta H_(rxn)=\sum [n* \Delta H_f(product)]-\sum [n* \Delta H_f(reactant)]`

`\Delta H_(rxn)=[(n_(H_2)* \Delta H_(H_2))+(n_(Ca(OH)_2)* \Delta H_(Ca(OH)_2))]-[(n_(Ca)* \Delta H_(Ca))+(n_(H_2O)* \Delta H_(H_2O))]`

where,

n = number of moles

As we know that standard enthalpy of an element and standard gas always be zero.

`\Delta H_(rxn)=[(n_(Ca(OH)_2)* \Delta H_(Ca(OH)_2))]-[(n_(H_2O)* \Delta H_(H_2O))]`

Now put all the given values in this expression, we get

`\Delta H_(rxn)=[(1mole* -986.09KJ/mole)]-[(2mole* -285.8KJ/mole)]\\\\\Delta H_(rxn)=-414.49KJ`

Therefore, the enthalpy change for this reaction is, -414.49 KJ