Question

In 1994, the sports league introduced a salary cap that limits the amount of money spent on players' salaries. The quadratic model y=0.2313x^2 + 2.600x + 35.17 approximates this cap in millions of dollars for the years 1994-2009, where x = 0 represents 1994 x = 1 represents 1995, and so on. Complete parts a and b.(A) Approximate the sports league salary cap in 2004.The approximate sports league salary cap in 2004 is $ 84.3 million(Completed)(Round to the nearest tenth as needed.)(B) According to the model, in what year did the salary cap reach 65 million dollars?According to the model, in ____ the salary cap reached 65 million dollars.(Round down to the nearest year.)Part A is completed so I just need help with Part B.

Answer 1

B) Given

`y=0.2313x^2+2.600x+35.17`

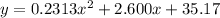
Set y=65 and solve for x, as shown below

`\begin{gathered} y=65 \\ \Rightarrow0.2313x^2+2.600x+35.17=65 \\ \Rightarrow0.2313x^2+2.600x-29.83=0 \end{gathered}`

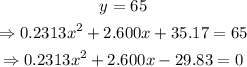
Then, solve the quadratic equation using the quadratic formula,

`\begin{gathered} x=(-2.600\pm√((2.600)^2-4*0.2313*-29.83))/(2*0.2313) \\ \Rightarrow x=-18.2915,7.05065 \end{gathered}`

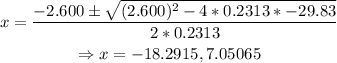
The function is not valid for negative values of x; therefore, the solution can only be x=7.05065 which can be rounded to x=7. Furthermore, x=7 corresponds to the year 2001. The answer to part B is 2001.