Question

The figures below are similar. What are a) the ratio of the perimeters and b) the ratio of the areas of the larger figure to the smaller figure? The figures are not drawn to scale.

Answer 1

a) ratio of the perimeters is the same as ratio of corresponding sides, so:


`(P_1)/(P_2)=k=(22)/(14)=(11)/(7)\approx1,57`

b) ratio of the areas is equal to k² so:


`(A_1)/(A_2)=k^2=\left((11)/(7)\right)^2=(121)/(49)\approx2,47`

Answer 2

a) Ratio of perimeters is 11:7

b) Ratio of area is 121:49

Explanation:

Given : Tho similar figures with sides 22 yd and 14 yd.

We have to find

a) the ratio of the perimeters and

b) the ratio of the areas of the larger figure to the smaller figure.

Consider the given figures,

a) Since, the ratio of perimeter of similar figures is same as the ratio of the corresponding sides of the figures.

That is Ratio of perimeter is same as ratio of sides of larger figure to smaller figure .

Mathematically ,

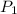`P_1` denotes perimeter of larger figure , and
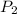`P_2` denotes perimeter of smaller figure

Thus,

`(P_1)/(P_2)= (22)/(14)=(11)/(7)`

Thus, Ratio of perimeters is 11:7

b) the ratio of the areas of the larger figure to the smaller figure.

The ratio of the areas of the two similar figures is the square of the ratio of the corresponding sides.

that is

`A_1` denotes area of larger figure , and
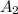`A_2` denotes area of smaller figure

Thus,
`(A_1)/(A_2)= (22^2)/(14^2)=(484)/(196)=(121)/(49)`

Thus,

`(A_1)/(A_2)=(121)/(49)`

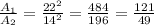
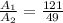
Thus, Ratio of area is 121:49