Answer:
Options B and D
Explanation:
Given that
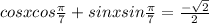
Use the formula for sum angles for Cos as
Cos A cos B +sin A sin B = cos (A-B)
we have
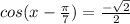
First let us solve principal solution
cos negative in the II quadrant
Hence principal soluton is
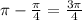 +
+
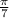
Again it is negative in third quadrant i.e. x =
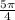 +
+
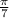
General solution is
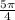 +
+
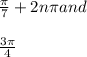 +
+
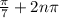
Options B and D