Question

Given a quadratic function, f(x) = ax 2 + bx + c has a negative leading coefficient and the vertex that has a negative y-coordinate. Determine the number of real zeros of the function. 2 real zeros 1 real zero 1 real zero and 1 imaginary zero 2 imaginary zeros

Answer 1

Answer D. 2 imaginary zeros

Answer 2

Answer with explanation:

The Given Quadratic function is

`f(x)=ax^2+b x +c`

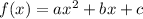
→The quadratic function has a negative leading coefficient and the vertex that has a negative y-coordinate.

→The given quadratic function when written , represents a parabola, opening downwards, and can lie either in third Quadrant or fourth Quadrant or in both.

→So, it can be written as

`y+k=(x\pm c)^2, {\text{Vertex}}=(\pm c, -k)`

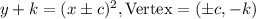
→If Vertex is (c,-k), still the Quadratic function or the parabola will have no real root, as Imaginary root occur in pairs,you can see the result from the image ,as function does not cross the x axis even once .

Similarly, If Vertex is (-c,-k), still the Quadratic function or a parabola will have no real root, as Imaginary root occur in pairs,you can see the result ,from the image ,as function does not cross the x axis even once .

So, the function has no real root.

Option D: 2 imaginary zeros