Question

At which points are the equations y = x2 + 3x + 2 and y = 2x + 3 approximately equal?

Answer 1

Use a system:


`2x+3=x^2+3x+2`


`0=x^2+x-1`


`x=0.618`


`x=-1.618`

Answer 2

The equations are approximately equals at the points
`(0.618,4.236)` and
`(-1.618,-0.236)`

Explanation:

we have

`y=x^(2)+3x+2` -----> equation A

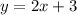`y=2x+3` -----> equation B

To solve the system of equations equate equation A to equation B

`x^(2)+3x+2=2x+3`

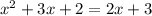
Group terms that contain the same variable

`x^(2)+3x-2x+2-3=0`

`x^(2)+x-1=0`

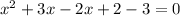
The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

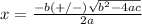
in this problem we have

`x^(2)+x-1=0`

so

`a=1\\b=1\\c=-1`

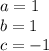
substitute in the formula

`x=\frac{-1(+/-)\sqrt{1^(2)-4(1)(-1)}} {2(1)}`

`x=\frac{-1(+/-)√(5)} {2}`

`x=(-1+√(5))/(2)=0.618`

`x=(-1-√(5))/(2)=-1.618`

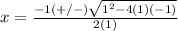
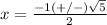
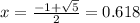
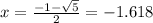
Find the values of y

For
`x=0.618`

`y=2(0.618)+3=4.236`

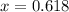
For
`x=-1.618`

`y=2(-1.618)+3=-0.236`

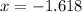
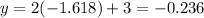
Therefore

The equations are approximately equals at the points
`(0.618,4.236)` and
`(-1.618,-0.236)`