Answer: The correct option is (C) Parallelogram.
Step-by-step explanation: Given that the co-ordinates of the vertices of a quadrilateral composed in the first quadrant of the coordinate plane are (0,0) (a, b), (a + c, b), and (c, 0).
We are to select the most accurate classification of the quadrilateral.
Let the co-ordinates of the vertices of the quadrilateral are P(0,0), Q(a, b), R(a + c, b), and S(c, 0).
The lengths of the sides are calculated using distance formula as follows :
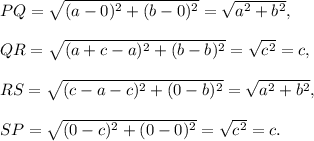
So, the opposite sides are equal in length.
And, the slopes of the sides are calculated as follows :

So, the slopes of the opposite sides are equal but
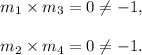
Thus, the opposite sides of the quadrilateral PQRS are equal and parallel and so PQRS is a PARALLELOGRAM.
Option (C) is CORRECT.