Question

Use the following compound interest formula to complete the problem. 2007-11-01-00-00_files/i0110000.jpg Victor has a credit card with an APR of 13.66%, compounded monthly. He currently owes a balance of $1,349.34. Assuming that Victor makes no purchases or payments, how much will he owe after one year, to the nearest cent? a. $1,349.34 b. $1,533.66 c. $1,545.65 d. $1,364.70

Answer 1

A=p (1+r/k)^kt
A=1,349.34×(1+0.1366÷12)^(12×1)
A=1,545.65

Answer 2

The correct answer is C. $ 1545.65

Explanation:

Principle = $ 1349.34

Rate = 13.66 %

t = No. of times the interest is compounded in one year

⇒ t = 12 ( since it is given that the interest is compounded monthly so the interest is compounded 12 times in one year)

n = 1 year

`Amount=Principle\cdot (1+(rate)/(n))^(n\cdot t)`

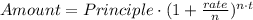
where n = no. of years and t = No. of times the interest is compounded in one year

`\Rightarrow Amount=1349.34\cdot (1+(13.66)/(100\cdot 12))^(12\cdot 1)`

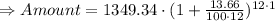
= 1349.34 × 1.15

= $ 1545.65

So, the correct answer is C