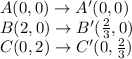Question

What would be the coordinates of triangle A'B'C' if triangle ABC was dilated by a factor of

1
3
?

Answer 1

`A(0,0)\rightarrow A'(0,0) \\ B(2,0)\rightarrow B'((2)/(3),0) \\ C(0,2)\rightarrow C'(0,(2)/(3))`

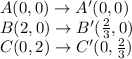
Explanation:

The question is as following:

The verticies of a triangle on the coordinate plane are

A(0, 0), B(2, 0) and C(0, 2).

What would be the coordinates of triangle A'B'C' if triangle ABC was dilated by a factor of 1/3 ?

=============================================

Given: the vertices of a triangle ABC are A(0, 0), B(2, 0) and C(0, 2).

IF the triangle is dilated by a factor of k about the origin, then

(x,y) → (kx , ky)

that triangle ABC was dilated by a factor of 1/3 to create the triangle A'B'C'.

It is given that triangle ABC was dilated by a factor of 1/3 to create the triangle A'B'C'.

If a figure dilated by a factor of 1/3 about the origin

So,
`(x,y)\rightarrow ((1)/(3)x,(1)/(3)y)`

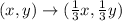
So, The coordinates of the triangle A'B'C' are:

`A(0,0)\rightarrow A'(0,0) \\ B(2,0)\rightarrow B'((2)/(3),0) \\ C(0,2)\rightarrow C'(0,(2)/(3))`