Question

Please help! Thank you

Brett deposited $3,200 into a savings account for which interest is compounded quarterly at a rate of 2. 4%.
How much interest will he earn after 15 years?

A) $300.42
B) $768.14
C) $1367.19
D) $1381.72

Answer 1

Find the future value
A=p (1+r/k)^kt
A=3,200×(1+0.024÷4)^(4×15)
A=4,581.72
interest earned
4,581.72−3,200
=1,381.72

Answer 2

D) $1381.72

Explanation:

We have been given that Brett deposited $3,200 into a savings account for which interest is compounded quarterly at a rate of 2. 4%. We are asked to find the amount of interest Brett will earn after 12 years.

We will use compound interest formula to solve our given problem.

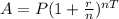`A=P(1+(r)/(n))^(nT)`, where,

A = Final amount after T years,

P = Principal amount,

r = Annual interest rate in decimal form,

n = Number of times interest is compounded per year,

T =Time in years.

Let us convert the given interest rate in decimal form.

`2.4\%=(2.4)/(100)=0.024`

Upon substituting our given values in above formula we will get,

`A=\$3200(1+(0.024)/(4))^(4*15)`

`A=\$3200(1+0.006)^(60)`

`A=\$3200(1.006)^(60)`

`A=\$3200*1.43178841202`

`A=\$4581.722918467\approx \$4581.72`

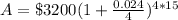
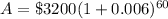
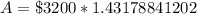
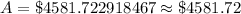
Now we will subtract $3200 from $4581.72 to find the amount of interest.

`\text{The amount of interest}=\$4581.72-\$3200`

`\text{The amount of interest}=\$1381.72`

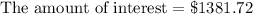
Therefore, Brett will earn $1381.72 in interest after 15 years and option D is the correct choice.