Question

If a polynomial function f(x) has roots 3 and square root of 7 what must also be a root of f(x)?

A negative square root of 7
B i square root of seven
C –3
D 3i

Answer 1

`-√(7)`

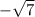
A is correct.

Explanation:

A polynomial function f(x) has root
`3\text{ and }√(7)`.

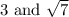3 is a real number.

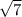`√(7)` is an irrational number.

The zeros or root of the function always occurs in conjugate pair.

Conjugate pair: A root has two form one positive and one negative.

e.g:
`a+√(b),a-√(b)`

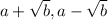
For the given function f(x),
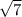`√(7)` should be in conjugate pair.

One more possible root would be
`-√(7)`

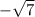
Hence, the one root must be negative of root of 7

Answer 2

Whenever you have a root of sqrt #, you must have the matching - (or positive).
This is because when you take a square root you get two solutions a positive and a negative.
The answer is LETTER A