Answer:
The surface area of the larger solid is 600 cm².
Explanation:
Since, when two solids are similar then the ratio of their corresponding measurement is the cube root of the ratio of their volumes,
Here, the volumes of two similar solids are 125 cm³ and 1,000 cm³,
Thus, the ratio in their corresponding measures =
![\sqrt[3]{(125)/(1000)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/y9kn42mh1fz7r42t5uuvlw5wf4y42xw8bt.png)
![=\frac{\sqrt[3]{125}}{\sqrt[3]{1000}}](https://img.qammunity.org/2018/formulas/mathematics/high-school/8b315vlphbk7ogkv6tfml6zyplot2aik2a.png)
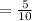
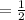
Also, the ratio of the surface areas of the similar solids is the square of the ratio of their corresponding measurement.
Thus, the ratio in their surface area =
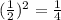
Given, the surface area of the smaller solid is 150 cm²,
Let A be the surface area of the larger solid,
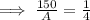

Hence, the surface area of the larger solid is 600 cm².