Question

A triangle has side lengths of 9 in, 13 in, and 20 in. What is the measurement of this triangle’s largest angle?

Answer 1

The Largest angle is 129.868 degrees

Answer 2

1. Given any triangle ABC with sides BC=a, AC=b and AB=c, the following are true :

i) the larger the angle, the larger the side in front of it, and the other way around as well. (Sine Law) Let a=20 in, then the largest angle is angle A.

ii) Given the measures of the sides of a triangle. Then the cosines of any of the angles can be found by the following formula:


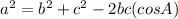
`a^(2)=b ^(2)+c ^(2)-2bc(cosA)`

2.


`image`

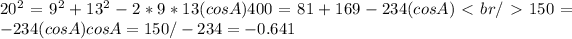
3. m(A) = Arccos(-0.641)≈130°,

4. Remark: We calculate Arccos with a scientific calculator or computer software unless it is one of the well known values, ex Arccos(0.5)=60°, Arccos(-0.5)=120° etc