The equation given is:
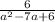
.
The second equation will have x as the unknown equivalent numerator with the denominator as (a-6)(a-1)(a+6).
Simplifying the second equation would result to:
/( a^(2) - 7a+6 )](https://img.qammunity.org/2018/formulas/mathematics/high-school/vz6evdv1yfmfvzz4pra02c7e66auw4ried.png)
Equating the two equations:
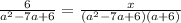
x = 6(a+6). The numerator of the equivalent equation is 6(a+6).