Question

Parallelogram FGHI on the coordinate plane below represents the drawing of a horse trail through a local park:

In order to build a scale model of the trail, the drawing is enlarged as parallelogram ABCD on the coordinate plane. If two corners of the trail are at point A (−2, 7) and point D (−10, −1), what is another point that could represent point B?

Answer 1

(10,7)

Explanation:

I took the test and got it right

Answer 2

The coordinates of B are (10,7).

Explanation:

It is given that the parallelogram ABCD is the image of Parallelogram FGHI. So, B is image of G.

Since FG is parallel to x-axis therefore AB is also parallel to x-axis and the y-coordinates of A and B are same.

Let the coordinates of B be (x,7).

Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`FI=√((2-4)^2+(-4-(-2))^2)=√(4+4)=√(8)=2√(2)`

`AD=√((-10-(-2))^2+(-1-7)^2)=√(64+64)=√(2(64))=8√(2)`

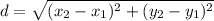
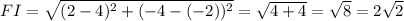
Scale factor of dilations is the proportion of side length of image and preimage.

`k=(AD)/(FI)=(8√(2))/(2√(2))=4`

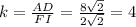
Length of AB is 4 times length of FG. The length of FG is

`FG=√((7-4)^2+(-2-(-2))^2)=√(3^2+0)=3`

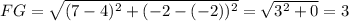
Length of AB is

`AB=4* FG=4* 3=12`

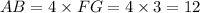
The points are A(-2,7) and B(x,7).

`AB=√((x-(-2))^2+(7-7)^2)`

`12=√((x+2)^2)`

`12=(x+2)`

`x=10`

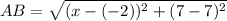
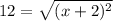
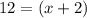
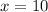
Therefore the coordinates of B are (10,7).