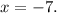Answer: The equation of directrices are
(1)
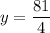
(2)
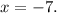
Step-by-step explanation: We are given to find the equation of the directrices of the following parabolas:
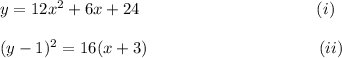
(1) The equation of the directrix for the parabola
 is given by
is given by
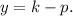
From equation (i), we have
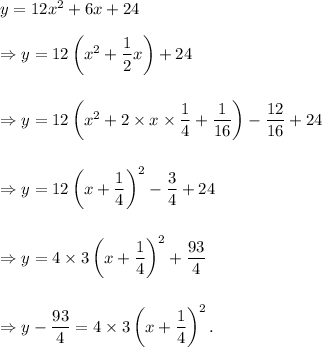
Comparing with the standard equation, we get
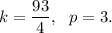
So, the equation of the directrix is
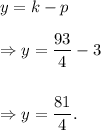
(2) The equation of the directrix for the parabola
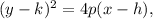 is given by
is given by
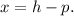
From equation (i), we have
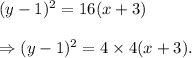
Comparing with the standard equation, we get
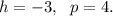
So, the equation of the directrix is
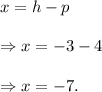
Thus, the equation of directrices are
(1)
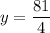
(2)