Question

A can in the shape of a right cylinder is filled with 10W-40 oil. The weight of 10W-40 oil is 0.857 gram per cubic centimeter. If the cylinder has a radius of length 6 cm and a height of 10 cm, calculate the weight of the oil (in grams) in the can. Round your answer to the nearest tenth.

Answer 1

To solve this, we have to find the volume of the cylinder first. The formula to be used is
`V = \pi r^(2) h`

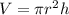
Given:V= ?r= 6cmh= 10cm
Solution:
`V = \pi r^(2) h`
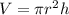
V= (3.14)(6cm)
`^(2)` x 10cmV= (3.14)(
`36cm^(2)`) x 10cmV= (
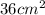
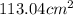
`113.04cm^(2)`) x 10cmV= 1130.4cm^3
Finding the volume of the cylinder, we can now solve what the weight of the oil is. Using the formula of density, Density = mass/volume, we can derive a formula to get the weight.
Given:Density = 0.857 gm/cm^3Volume = 1130.4 cm^3
Solution:weight = density x volumew= (0.857 gm/cm^3) (1130.4cm^3)w= 968.7528 gm
The weight of the oil is 968.75 gm.