Question

This one is super hard

Answer 1

We are given the following sequence:

`7,10,13`

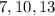
We notice that each term is determined by adding 3 to the previous, therefore, this is an arithmetic sequence and the common difference is 3. The nth term of an arithmetic sequence is:

`a_n=a_1+(n-1)d`

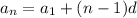
Where a1 is the first term and "d" is the common difference. Replacing the values we get:

`a_n=7+(n-1)(3)`

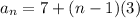
Simplifying:

`\begin{gathered} a_n=7+3n-3 \\ a_n=4+3n \end{gathered}`

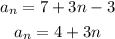
Now we replace n = 33 in the formula:

`\begin{gathered} a_(33)=4+3(33) \\ a_(33)=4+99 \\ a_(33)=103 \end{gathered}`

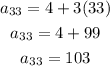
Therefore, the 33rd term is 103.