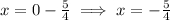Question

A parabola is represented by the equation y2 = 5x. Which equation represents the directrix? 

y = –20

x = –20 y = -5/4 x = -5/4

Answer 1

On ed its x = -5/4

Explanation:

Answer 2

`x=-(5)/(4)`

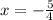
Explanation:

Given equation,

`y^2=5x-----(1)`

Which is the equation of a parabola along x-axis,

From equation (1),

`(y-0)^2=(4)/(4)* 5(x-0)`

`(y-0)^2=4((5)/(4))(x-0)-----(2)`

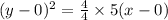
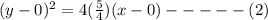
We know that, the standard form of a parabola along x-axis is,

`(y-k)^2=4p(x-h)`

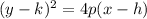
Where, the directrix is,

x = h-p

By comparing equation (2),

The directrix of the given parabola is,

`x = 0 - (5)/(4)\implies x = -(5)/(4)`