Question

The total number of pairs of integers (x,y) which satisfy the equation x^2-4xy+5y^2+2y-4=0 is?

Answer 1

Interesting and not very easy question.
First, we have to complete the squares for x and y and rewrite this equation in "standard" form.


`x^2-4xy+5y^2+2y-4=0\\\\x^2-4xy+4y^2+y^2+2y-4=0\\\\\big(x^2-2\cdot x\cdot2y+(2y)^2\big)+y^2+2y-4=0\\\\(x-2y)^2+y^2+2y+1-1-4=0\\\\(x-2y)^2+(y^2+2y+1)-5=0\\\\\boxed{(x-2y)^2+(y+1)^2=5}`

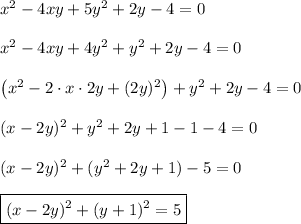
x and y are integers and we know that if two numbers a and b are integers then (a+b), (a-b), a*b are integers too, so (x-2y) and (y+1) from our equation, are integers.

In equation, we add two squares and get 5 as result. This is possible only when we have:

1² + 2² = 1 + 4 = 5
or
2² + 1² = 4 + 1 = 5

If so, there will be:

1.


`1+4=5\\\\ (x-2y)^2+(y+1)^2=5 \implies(x-2y)^2=1\quad\wedge\quad(y+1)^2=4\\\\\\ (y+1)^2=4\\\\(y+1)=2\quad\vee\quad (y+1)=-2\\\\y=2-1\quad\vee\quad y=-2-1\\\\\boxed{y=1\quad\vee\quad y=-3}\\\\`

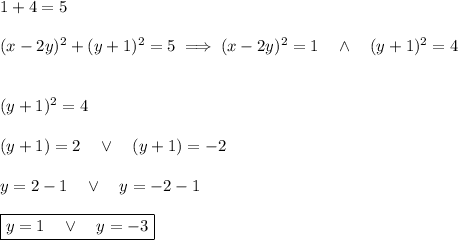
For y = 1


`(x-2y)^2=1\\\\(x-2y)=1\quad\vee\quad(x-2y)=-1\\\\(x-2\cdot1)=1\quad\vee\quad(x-2\cdot1)=-1\\\\x-2=1\quad\vee\quad x-2=-1\\\\x=1+2\quad\vee\quad x=-1+2\\\\\boxed{x=3\quad\vee\quad x=1}`

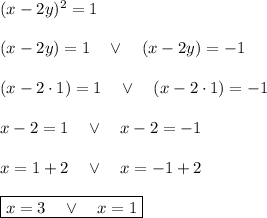
we have two pairs (3,1) and (1,1).

For y = -3


`(x-2y)^2=1\\\\(x-2y)=1\quad\vee\quad(x-2y)=-1\\\\(x-2\cdot(-3))=1\quad\vee\quad(x-2\cdot(-3))=-1\\\\x+6=1\quad\vee\quad x+6=-1\\\\x=1-6\quad\vee\quad x=-1-6\\\\\boxed{x=-5\quad\vee\quad x=-7}`

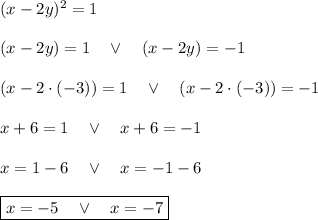
we have two pairs (-5,-3) and (-7,-3).

2.


`4+1=5\\\\ (x-2y)^2+(y+1)^2=5 \implies(x-2y)^2=4\quad\wedge\quad(y+1)^2=1\\\\\\ (y+1)^2=1\\\\(y+1)=1\quad\vee\quad (y+1)=-1\\\\y=1-1\quad\vee\quad y=-1-1\\\\\boxed{y=0\quad\vee\quad y=-2}`

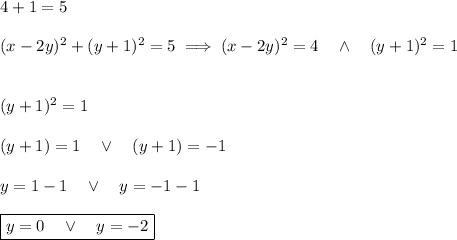
For y = 0


`(x-2y)^2=4\\\\(x-2y)=2\quad\vee\quad(x-2y)=-2\\\\(x-2\cdot0)=2\quad\vee\quad(x-2\cdot0)=-2\\\\\boxed{x=2\quad\vee\quad x=-2}`

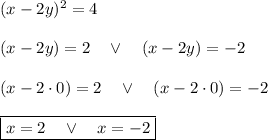
we have two pairs (2,0) and (-2,0)

For y = -2


`(x-2y)^2=4\\\\(x-2y)=2\quad\vee\quad(x-2y)=-2\\\\(x-2\cdot(-2))=2\quad\vee\quad(x-2\cdot(-2))=-2\\\\x+4=2\quad\vee\quad x+4=-2\\\\x=2-4\quad\vee\quad x=-2-4\\\\\boxed{x=-2\quad\vee\quad x=-6}`

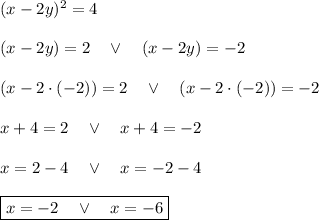
we have two pairs (-2,-2) and (-6,-2).

So the total number of pairs of integers which satisfy the equation is 8.