Question

What is the coefficient of x in expansion of (x+3)^5 ?

Answer 1

Consider the binomial expansion of (1 + x)ⁿ, which is the binomial theorem.


`(1 + x)^(n) = \sum_(r = 0)^(n)\left(\begin{array}{ccc}n\\r\end{array}\right)(1)^(n - r)(x)^(r)`

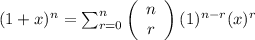
Thus, we can say that the expansion of (3 + x)⁵ is:


`(3 + x)^(5) = \sum_(r = 0)^(5)\left(\begin{array}{ccc}5\\r\end{array}\right)(3)^(5 - r)(x)^(r)`

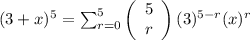
We can see that the only way to have an x-value in the expansion is when r = 1. Substituting r = 1 into the expansion, we get:


`\text{Coefficient of x: }\left(\begin{array}{ccc}5\\1\end{array}\right)(3)^(5 - 1)`

`= 5 \cdot 3^(4)`

`= 5 \cdot 81`

`= 405`

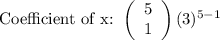
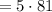
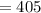
Thus, the coefficient of the x term is 405, based on our binomial theorem.

Answer 2

Answer:
Coefficient is 405.