Answer:
C) 212,000 years
Step-by-step explanation:
The half-life of a radioactive sample is the time it takes for half of the sample to decay.
In this case, the half-life is 53,000 years: this means that after 53,000 years, half of the sample will decay. So we will have:
- After 1 half life (53,000 years): 1/2 of the sample has decayed, so 1/2 is left undecayed
- After 2 half-lives (106,000 years): since the amount left is now 1/2, the amount that decay now is
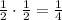 . So the total amount decayed is now
. So the total amount decayed is now
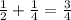 , and the amount left is
, and the amount left is
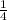
- After 3 half-lives (159,000 years): since the amount left is now 1/4, the amount that decay now is
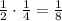 . So the total amount decayed is now
. So the total amount decayed is now
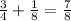 , and the amount left is
, and the amount left is
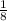
- After 4 half-lives (212,000 years): since the amount left is now 1/8, the amount that decay now is
 . So the total amount decayed is now
. So the total amount decayed is now
 , and the amount left is
, and the amount left is
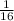
So, the correct answer is
C) 212,000 years