We are given that a tree casts a shadow of 47.2 feet and we are asked to determine its height. We are also given that a yardstick cast a shadow of 3.5 feet. The yardstick and the tree form right triangles as shown in the next diagram:
Since both the tree and the yardstick have the same angle of incidence of light this means that both triangles are similar triangles, and therefore, we have the following relationship:
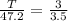
This is, the ratio between the opposite side and the adjacent sides of both triangles is the same. Now we solve for T by multiplying both sides by 47.2:
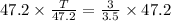
Solving the operations:
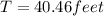
Therefore, the height of the tree is 40.46 feet.
For the second part we have:
If the tree falls then the length of 40.46 feet wouldn't be enough to hit the garage.