Answer:
Volume of the new cube is
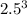 times larger than the original cube.
times larger than the original cube.
Explanation:
We are given that,
A cube is dilated by a factor of 2.5.
Let, the length of the sides of the original cube = x units.
Thus, we have,
Volume of the original cube =
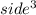
i.e. Volume of the original cube =

Now, as the original cube is dilated by a factor of 2.5
Then, the length of the sides of the new cube will be '2.5x' units.
Thus, Volume of the new cube =
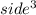
i.e. Volume of the new cube =
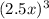
So, the factor by which volume of the new cube is larger than the volume of the original cube is,
Factor =
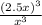
i.e. Factor =
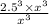
i.e. Factor =
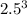
Hence, the volume of the new cube is
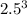 times larger than the original cube.
times larger than the original cube.