Question

A cube is dilated by a factor of 2.5.

How many times larger is the volume of the resulting cube than the volume of the original cube?



Enter your answer as a decimal in the box.

Answer 1

It should be 2.5³
Which should equal to 15.625

Answer 2

`(2.5)^(3)`

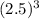
Explanation:

Given : A cube is dilated by a factor of 2.5.

To Find: How many times larger is the volume of the resulting cube than the volume of the original cube?

Solution :

Let the length of the sides of the original cube = x units.

Formula of volume of cube
`=a^(3)`

Where a is the side of cube

So, Volume of the original cube
`=x^(3)`

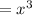
Since we are given that the original cube is dilated by a factor of 2.5

So, the length of the side of the dilated cube will be '2.5x' units.

Thus, Volume of the new cube
`=(2.5x)^(3)`

The factor by which volume of the new cube is larger than the volume of the original cube is:

Factor =
`((2.5x)^(3))/(x^(3))`

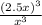
Factor =
`((2.5)^(3)*x^(3))/(x^(3))`

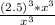
Factor =
`(2.5)^(3)`

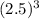
Hence the volume of the new cube is
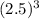`(2.5)^(3)` of the original cube

i.e. Factor =

i.e. Factor =

Hence, the volume of the new cube is times larger than the original cube.